Can I Use This Method? (for Coastal Inundation Assessment)
- Matt Eliot
- Jan 26, 2023
- 6 min read
Updated: Jul 15, 2025
Techniques for the evaluation of coastal inundation likelihood have progressively advanced from the analysis of high water level records using purely stochastic methods, through to detailed numerical modelling, built around the concept of synthetic storm databases. A key reason for this refinement has been the desire to represent increasingly extreme events, requiring far greater precision. The progressive refinement of the assessment methods can be associated with a set of constraints, each of which has led to development of a specific technique (Figure 1). For modern practice, the importance of these steps is to suggest the conditions under which less refined methods may be applicable, which is useful due to the relatively lower information needs and corresponding cost. Consequently, a wide variety of methods to estimate storm water levels remain in present use. The largest single distinction between assessment types is the use of either data analysis techniques (interpreted statistically) or numerical modelling, where observational data is used for model calibration or validation.
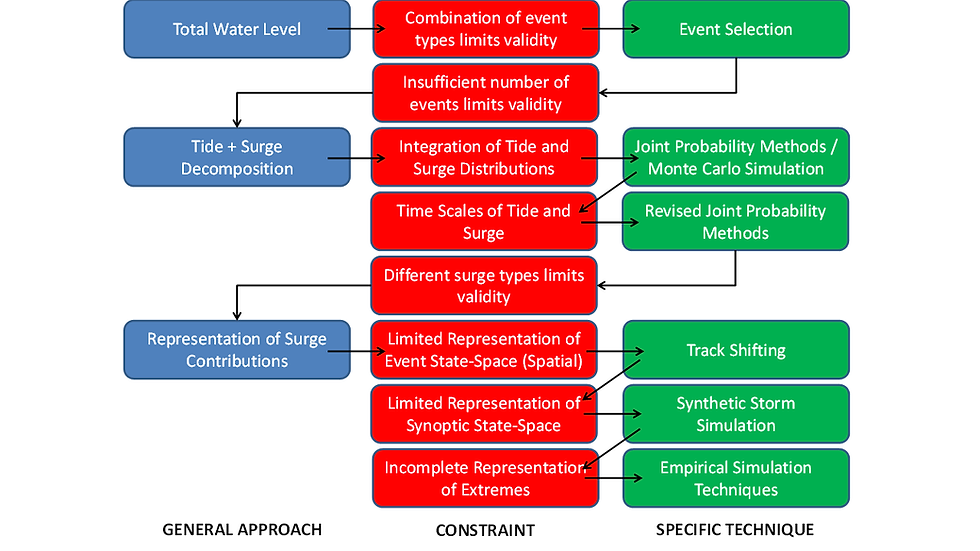
Figure 1: Refinement of Coastal Inundation Methods due to Technical Constraints
Refinement of coastal inundation methods (Figure 1) can be related to a number of broad trends corresponding to increased complexity in coastal science, including:
A shift from description of site-specific observations, through spatial or temporal interpolation, to the use of observations as validation for numerical modelling;
Movement from statistical and analytic models to increased use of numerical models; and
Evaluation of increasingly unusual (extreme) water level phenomena.
However, progressive decomposition of water level signals has been the key mechanism used to introduce greater complexity to coastal inundation assessment. It is therefore the key attribute described in the ‘General Approach’ in Figure 1. Decomposition has shifted from the analysis of total water level observations (up to the 1950s), through tide-surge separation, to representation of multiple surge components (from the 1990s). As the introduction of complexity comes with greater cost, and not always greater precision, simpler approaches continue to be valuable.
Analysis of total water levels allowed identification of key processes such as tides 13 and water level response to storm events [i]. However, the highly skewed nature of extreme water level events challenged their description using commonly applied statistics. The introduction of statistical methods to consider extremes [ii] was followed by application to extreme total water levels [iii]. Although there have been subsequent refinement to accommodate different means of sampling [iv] and techniques to consider a wider range of skew, the methods of Extreme Value Analysis remain highly important to coastal inundation assessment [v],[vi].
The majority of water level variation is predictable, due mainly to the influence of astronomic tides. This allows separation of the total water level signal into deterministic and non-deterministic components (tides and residuals). Further distinction between slowly and rapidly changing non-deterministic components provides the basis for the commonly used decomposition into tide, surge and mean sea level variations.
Distinction of the three components may allow for:
Treatment of water level signals that are peculiar to the period of observation, and therefore would bias extrapolation to longer time frames; and
Better inclusion of modelling outputs, particularly because surge, tide and mean sea level generally use different models.
A long-term probability distribution for each of the components is then recombined to estimate the likelihood of extreme events, such as the joint probability method [vii].
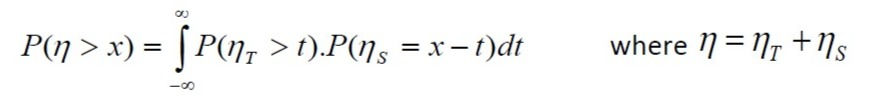
Where h is total water level, ht and hs are tide and surge components respectively.
This approach provides improved confidence when estimating extremes compared to a statistical fit to total water level data, as it uses a greater sample set from each of the components to generate the likelihood [viii] (Figure 2). A constraint with this approach is that distributions are dependent on sampling time scale, leading to the revised joint probability method, which accounts for storm surge / tide duration [ix].
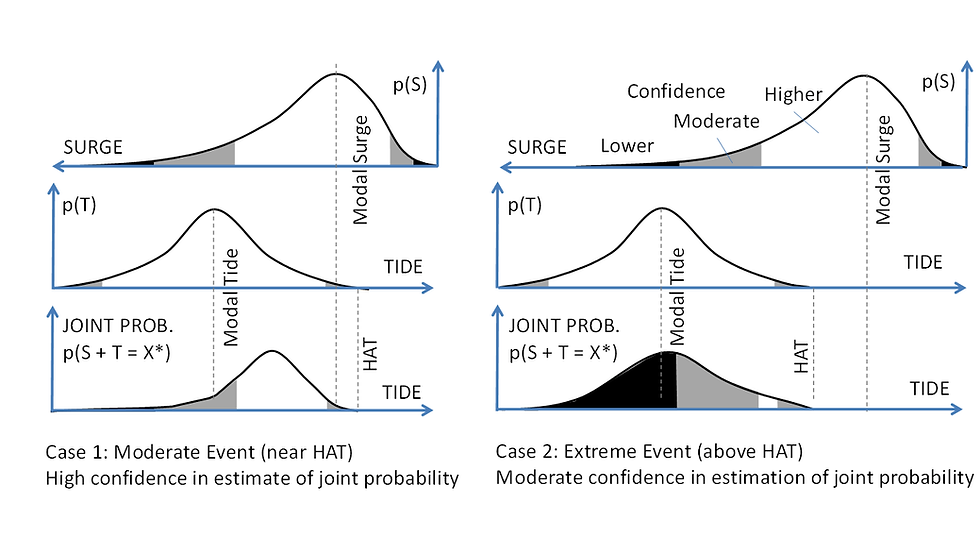
Figure 2: Basis for Improved Confidence with Joint Probability
Development of the long-term surge distribution is generally the most problematic component. The non-deterministic nature of surge, its small scales of variation and heavily skewed distribution determine that there are generally only a small number of events that represent extreme conditions within an observational data set [x].
The effects of sub-sampling from a tropical cyclone database should be considered carefully. This may neglect events from a critical path, or fail to capture low-moderate surges, and therefore provide a limited domain of model validity (Figure 3a). This domain may be further reduced if tide and surge distributions are integrated following the model, rather than as part of the Monte Carlo process (Figure 3b). Typically the upper limit of the surge model (Su2) is considered infinite, as small probabilities only provide small error to total water level likelihood.

Figure 3: Domain of Validity and Tide-Surge Integration
For tropical storms, the local nature of surges significantly complicates the ability to transfer surge estimates between locations. For the Western Australian coast this is illustrated by the difference of estimated extreme water level distributions at Karratha and Dampier, due to their relative locations on the Burrup Peninsula. Spatially-varying surge response was a major reason for shifting from point-based analysis of water level observations through to the use of numerical modelling. In effect, this is another form of decomposition, as each of the individual components of storm surge, such as pressure response, wind setup or wave setup, are able to be individually represented by a hydrodynamic model.
Methods to Assess Coastal Inundation Likelihood
Selection of an appropriate method for water level assessment requires an understanding of the degree of certainty desired, and the availability of supporting data. In general, more advanced methods provide improved certainty. However, degrees of freedom in modelling practice or limited data availability to support validation determine that potentially unacceptable uncertainty can be associated with even highly refined estimates of extreme water level likelihood. In all cases, definition of ‘hard’ flooding criteria based on flood likelihood estimates should be used with great care, and the practice of evaluating receptor sensitivity to events larger than design thresholds should be applied [xiii],[xiv],[xv],[xvi].
Some important factors influencing the choice of assessment methods may include:
Limitations of available data – in terms of the range of events observed, the type of historic information recorded and its quality, to support either statistical analysis or model validation;
Scale of process – required to cover the area of interest with a practical time and budget;
Model algorithms – must be suitable to the site and range of forcing mechanisms, such as cases where it is appropriate to include both land crossing and shore parallel storm systems;
Uncertainty of climate – capacity to represent inter-annual and decadal scale climate fluctuations, in addition to projected trends in climate change;
Tide, mean sea level and wave interactions – the manner in which these phenomena interact with surge requires careful representation, as demonstrated by development of the revised joint probability method.
[i] Proudman J. (1954). Note on the Dynamics of Storm‐Surges. Geophysical Journal International, 7(s1), 44-48. [ii]Weibull WA. (1951) A statistical distribution function of wide applicability. Journal of Applied Mechanics, 18: 292-297 [iii]Gumbel EJ. (1954) Statistical Theory of Extreme Values and Some Practical Applications. National Bureau of Standards, Applied Mathematics Series, 33. [iv]Petrauskas C & Aagaard P. (1971) Extrapolation of Historical Storm Data for Estimating Design Wave Heights. Society of Petroleum Engineers Journal. 251: 23-37 [v]Bruun JT & Tawn JA. (1998) Comparison of approaches for estimating the probability of coastal flooding. Applied Statistics, 27 (3): 405-423. [vi] Arns A, Wahl T, Haigh ID, Jensen J & Pattiaratchi C. (2013). Estimating extreme water level probabilities: a comparison of the direct methods and recommendations for best practise. Coastal Engineering, 81, 51-66. [vii]Pugh D & Vassie J. (1980) Applications of the joint probability method for extreme sea level computations. Proceedings of the Institution of Engineers, 9: 361-372. [viii]Middleton J & Thompson K. (1986) Return Periods of Extreme Sea Levels From Short Records. Journal of Geophysical Research, 91 (10): 11707-11716. [ix]Dixon MJ & Tawn JA. (1999) The effect of non-stationarity on extreme sea-level estimation. Journal of the Royal Statistical Society. Series C (Applied Statistics), 48 (2): 135-151. [x]Oumeraci H. (2005) Integrated Risk-Based Design and Management of Coastal Flood Defences. In : (Ed) Hofstede J. (2005) COMRISK. Common Strategies to Reduce the Risk of Storm Floods in Coastal Lowlands. Die Kuste Special Edition, 70: 151-172. [xi] United States Army Corps of Engineers. (2002) Coastal Engineering Manual. Engineer Manual 1110-2-1100, US Army Corps of Engineers. [xii] Intergovernmental Oceanographic Commission. (2006) Manual on Sea-level Measurements and Interpretation, Volume IV: An update to 2006. Paris, Intergovernmental Oceanographic Commission of UNESCO. 78 pp. IOC Manuals and Guides No.14, vol. IV ; JCOMM Technical Report No.31; WMO/TD. No. 1339. [xiii] ARMCANZ (2000) Floodplain management in Australia – best practice principles and guidelines. Agriculture and Resource Management Council of Australia and New Zealand, Standing Committee on Agriculture and Resource Management, Report No 73, CSIRO Publishing, Collingwood, Victoria. [xiv] Ale BJM. (2005) Risk is of all Time. In: (Ed) Hofstede J. (2005) COMRISK. Common Strategies to Reduce the Risk of Storm Floods in Coastal Lowlands. Die Kuste Special Edition, 70: 173-184. [xv] Balmforth D, Digman C, Kellagher R & Butler D. (2006) Designing for exceedance in urban drainage – good practice. CIRIA C635. [xvi] Australian Emergency Management Institute. (2013) Managing the floodplain - a guide to best practice in flood risk management in Australia. Handbook 7, Australian Emergency Management Handbook Series. National Strategy for Disaster Resilience.




Comments